Coordinate system
This page briefly covers Mach’s coordinate systems; then it delves into traversing coordinate systems explaining at a high-level (and with very minimal maths) how e.g. a polygon in a 3D model in the scene goes through a bunch of coordinate system transforms before finally ending up as a pixel on the screen.
You don’t have to read this whole page, but it might be worth skimming and taking a look at the diagrams!
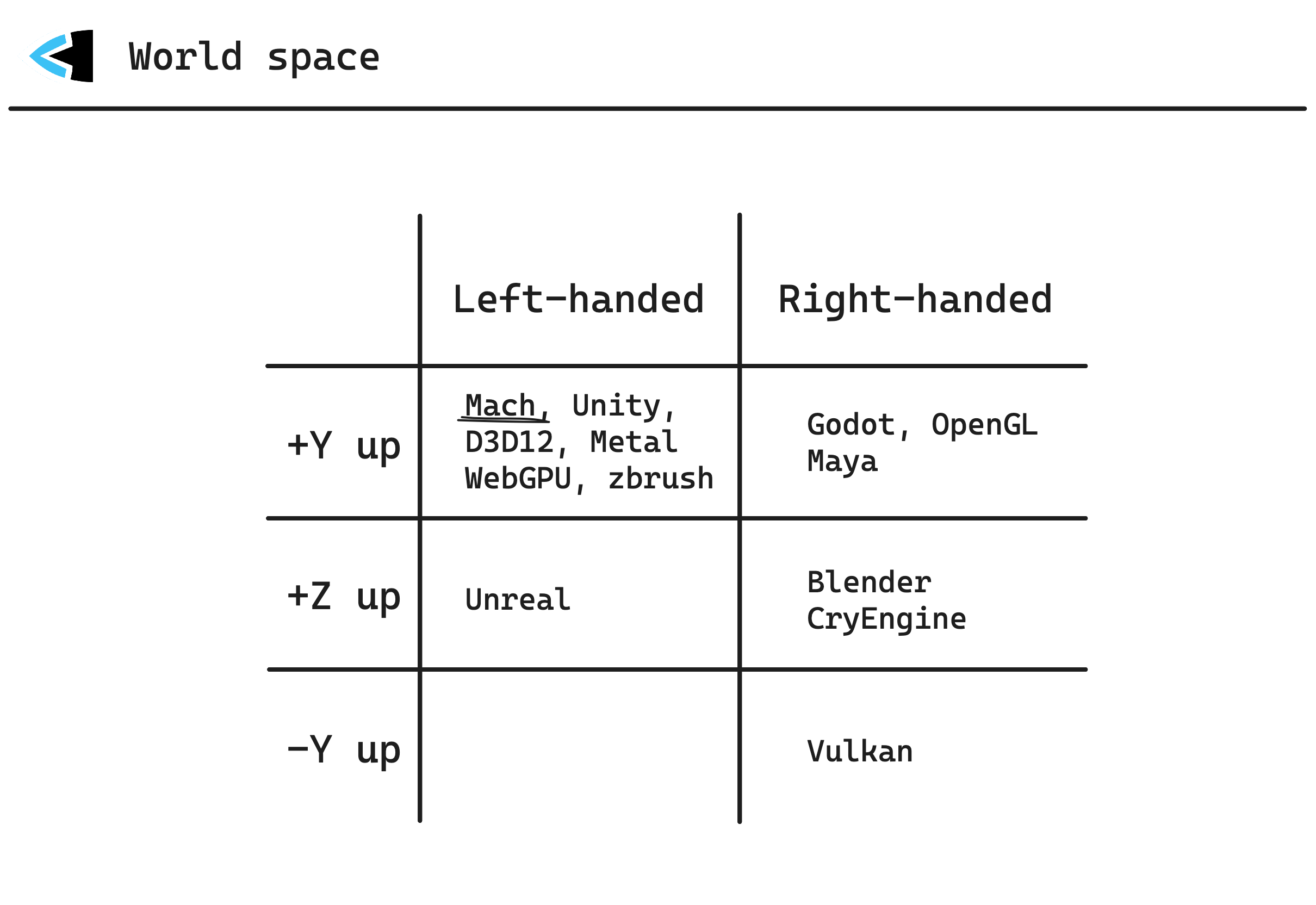
World space
3D models and 2D sprites are said to exist in world space, Mach uses a ‘+Y up, left-handed’ coordinate system to represent objects in space. To visualize it, imagine your own eyes are the camera. Hold your left hand out in front of you in a thumbs-up pose, as if you were holding a stick:
- X goes through the back side of your palm, towards your fingernails
- Y goes through the bottom of your hand towards the tip of your thumb
- Z goes through your eyes and towards your thumb
- Positive rotation values follow the direction of your fingers curled around the stick (any axis)
Quick reference
| What | Coordinate system |
|---|---|
| World space | +Y up, left-handed |
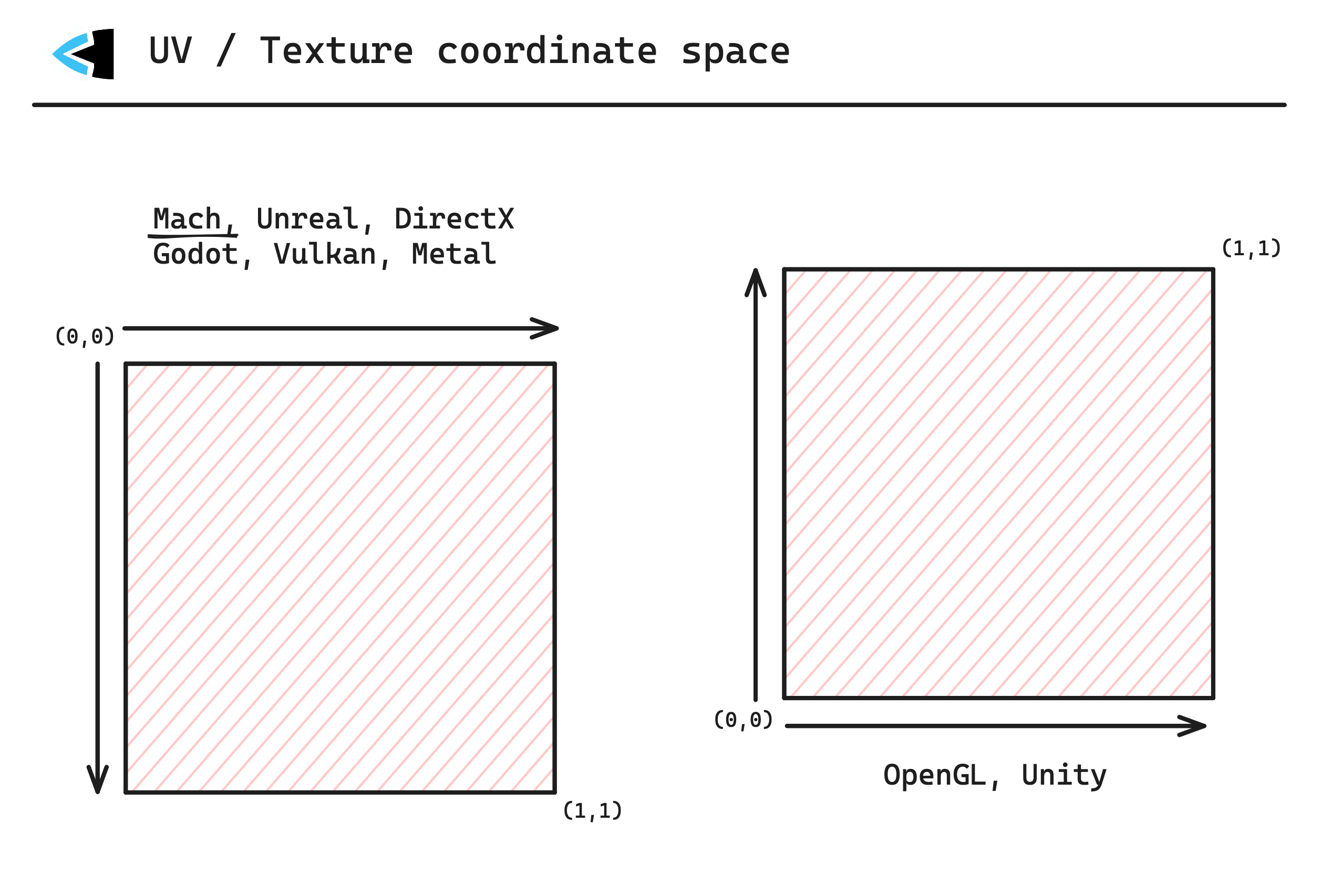
| Texture coordinates | +Y down; (0, 0) is at the top-left corner and the first texel in memory address order. (1, 1) is the last texel in memory address order. |
| Framebuffer coordinates | +Y down; (0, 0) is at the top-left corner |
| Normalized device coordinates (NDC) | +Y up; (-1, -1) is at the bottom-left corner |
Mach vs. other software
If you are familiar with other software / APIs, the following comparison tables may be helpful:
Traversing coordinate systems
Ever wondered how a vertex on a 3D model in a scene ultimately ends up on the 2D screen? We’ll walk through the various coordinate system transformations involved in that in the next section: traversing coordinate systems


 Donate
Donate